Propagation d'une onde lumineuse
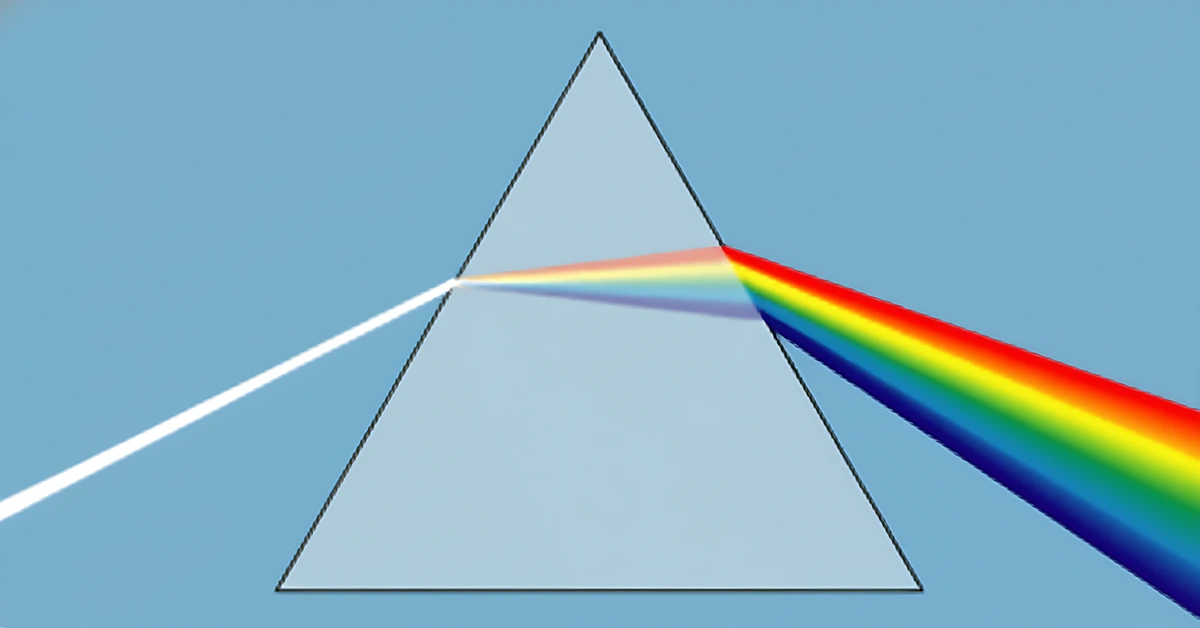
Diffraction de la lumière
Le phénomène de diffraction montre que la lumière possède un comportement ondulatoire. Elle peut donc être décrite, comme toute onde, à l’aide de trois grandeurs fondamentales : sa célérité, sa fréquence et sa longueur d’onde.
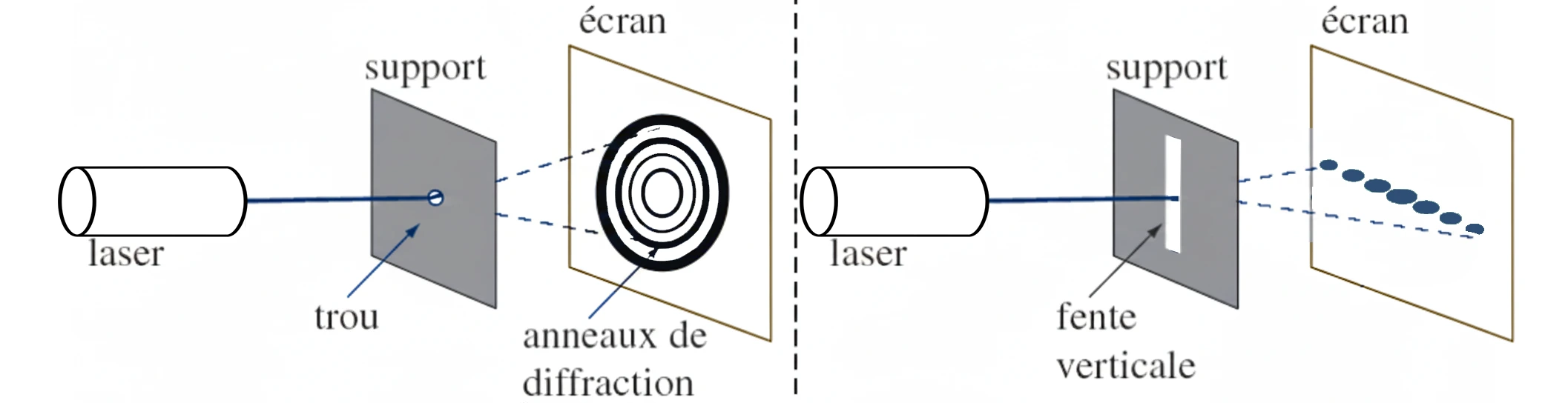
Étude de la diffraction d’un faisceau laser par une fente
L’écart angulaire \( \theta \) est l’angle sous lequel on observe la moitié de la tache centrale depuis la fente de diffraction.
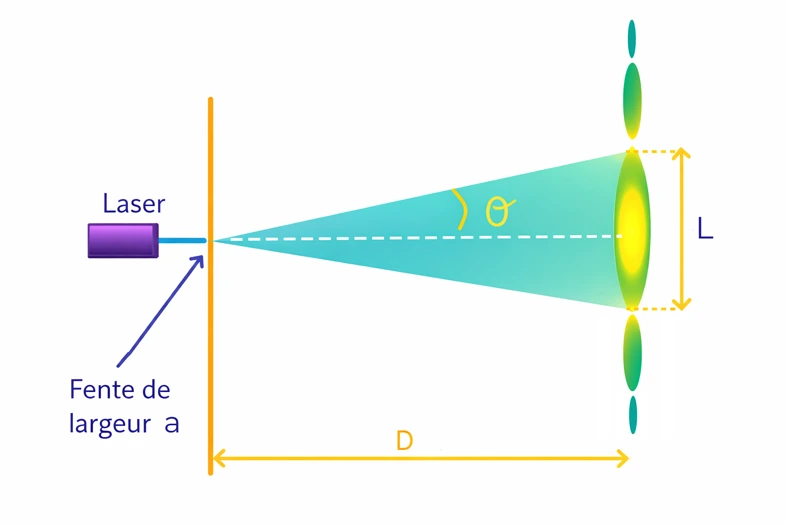
Il est défini par la relation :
\[ \theta = \frac{\lambda}{a} \]À partir du schéma expérimental, on a :
\[ \tan \theta = \frac{L}{2D} \]Pour des angles petits (exprimés en radians), on peut utiliser l’approximation :
\[ \tan \theta \approx \theta \]D’où :
\[ \theta = \frac{L}{2D} \]En combinant les deux expressions précédentes, on obtient :
\[ \frac{\lambda}{a} = \frac{L}{2D} \]Caractéristiques des ondes lumineuses
La lumière n’est pas une onde mécanique, mais une onde électromagnétique. Elle peut se propager dans les milieux transparents ainsi que dans le vide.
Sa vitesse de propagation dépend du milieu traversé :
- Dans le vide (et l’air) : \( c = 3{,}0 \times 10^{8}\ \text{m·s}^{-1} \)
- Dans le verre : \( v_{\text{verre}} \approx 2{,}0 \times 10^{8}\ \text{m·s}^{-1} \)
- Dans l’eau : \( v_{\text{eau}} \approx 2{,}25 \times 10^{8}\ \text{m·s}^{-1} \)
Lumière monochromatique
Une radiation lumineuse de couleur unique est dite monochromatique. Elle est caractérisée par une fréquence \( \nu \) constante, quelle que soit la nature du milieu traversé.
Exemple : le laser, qui constitue une source typique de lumière monochromatique.
Lumière polychromatique
La lumière blanche visible est polychromatique : elle résulte de la superposition de plusieurs radiations monochromatiques.
C’est le cas de la lumière du Soleil, d’une lampe à incandescence ou d’une bougie.
Le domaine du visible s’étend approximativement de :
\[ 400\ \text{nm} \leq \lambda \leq 800\ \text{nm} \]Dispersion des ondes lumineuses
Indice de réfraction
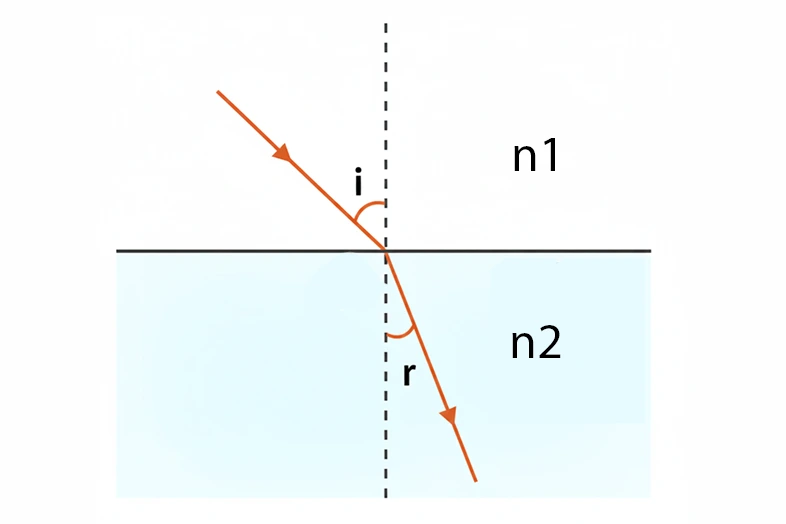
Chaque milieu transparent est caractérisé par son indice de réfraction \( n \), défini par :
\[ n = \frac{c}{v} \]où :
- \( c \) : vitesse de la lumière dans le vide (\( c = 3{,}0 \times 10^{8}\ \text{m·s}^{-1} \))
- \( v \) : vitesse de la lumière dans le milieu considéré
Dans le vide :
\[ c = \lambda_0 \, \nu \]Dans un milieu donné :
\[ v = \lambda \, \nu \]D’où la relation :
\[ n = \frac{c}{v} = \frac{\lambda_0}{\lambda} \]Le prisme
Un prisme est un milieu transparent et homogène, limité par deux faces planes non parallèles formant un angle \( A \), appelé angle du prisme.
La face opposée à l’arête principale est appelée la base du prisme.
Loi de réfraction de Descartes
Lorsqu’un rayon lumineux traverse la frontière entre deux milieux transparents, il change de direction. Cette déviation obéit à la loi de réfraction de Descartes :
\[ n_1 \sin i = n_2 \sin r \]Relations caractéristiques du prisme
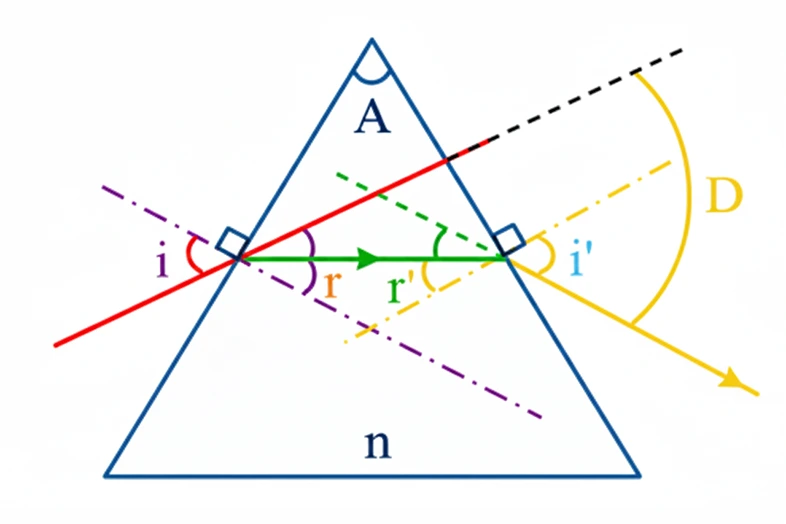
Pour un prisme, on utilise les relations suivantes (à retenir) :
- \( \sin i = n \sin r \)
- \( \sin i' = n \sin r' \)
- \( A = r + r' \)
- \( D = i + i' - A \)
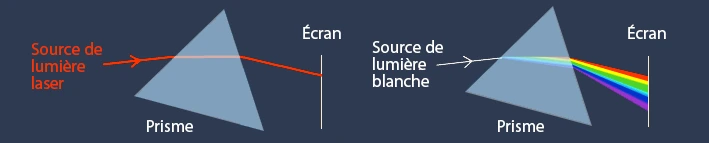
Dispersion de la lumière par le prisme
Lorsqu’un faisceau de lumière blanche traverse un prisme, on observe la séparation des différentes couleurs, comme dans un arc-en-ciel.
L’ensemble des couleurs obtenues constitue le spectre de la lumière blanche.
On dit alors que la lumière blanche a été dispersée.
Observation expérimentale :
- La lumière violette est la plus déviée,
- La lumière rouge est la moins déviée.
Le prisme dévie différemment chaque radiation monochromatique, ce qui permet leur séparation : c’est le phénomène de dispersion de la lumière blanche.
