2ème Année Bac BIOF Physique-Chimie (SPC) Physique

Ondes mécaniques progressives périodiques

Définition d’une onde mécanique progressive périodique – sinusoïdale

Une onde mécanique progressive périodique est une onde dans laquelle l’évolution temporelle de la perturbation de chaque point du milieu de propagation est périodique.

Elle est dite sinusoïdale lorsque l’évolution temporelle de la source peut être associée à une fonction sinusoïdale.

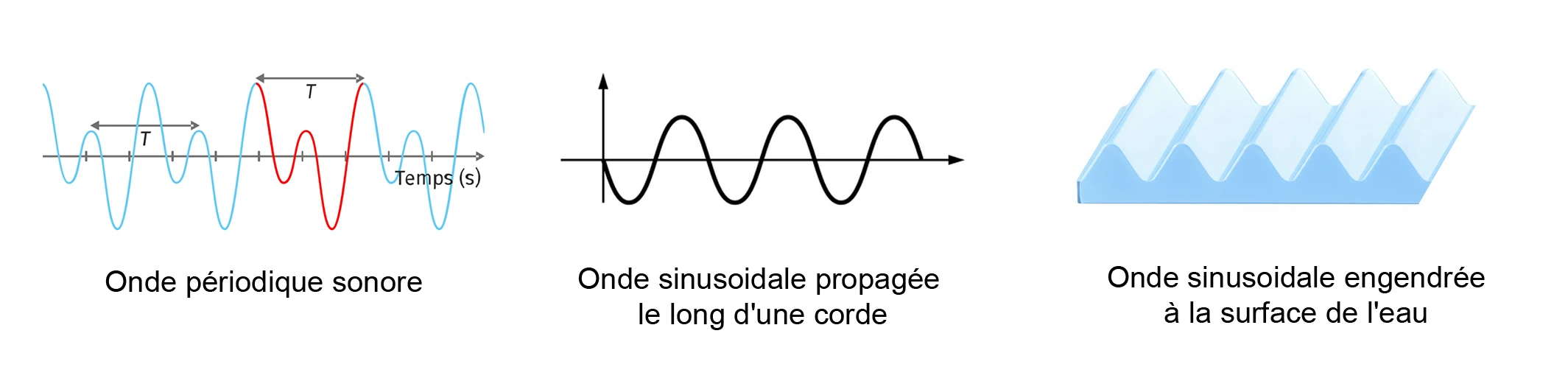
Exemples :

Onde périodique sonore (ex. : son d’un diapason),
Onde sinusoïdale propagée le long d’une corde vibrante,
Onde sinusoïdale à la surface de l’eau (rides circulaires régulières).

Caractéristiques d’une onde mécanique progressive périodique

Une onde mécanique progressive périodique se décrit à l’aide de grandeurs temporelles et spatiales :

Période temporelle $T$ : c’est la plus petite durée au bout de laquelle la perturbation se reproduit identique à elle-même en un point donné.
Longueur d’onde $λ$ : c’est la plus petite distance séparant deux points successifs ayant le même état de vibration (même élongation et même vitesse).
Fréquence $N$ (ou $f$ , $ν$ ) : c’est le nombre de périodes par unité de temps. Elle est liée à la période par la relation :

N = \frac{1}{T}

Vitesse de propagation

La vitesse de propagation $V$ d’une onde mécanique progressive périodique est donnée par :

V = \frac{λ}{T} = λ N

avec : $V$ en m·s $^{- 1}$ , $λ$ en m, $T$ en s, et $N$ en Hz.

Mesure à l’aide d’un stroboscope

Le stroboscope émet des éclairs périodiques de fréquence réglable $N_{s}$ . Lorsque $N_{s} = N$ , l’onde apparaît immobile (ou animée d’un mouvement très lent) : c’est le phénomène d’immobilité apparente. Dans ce cas, la fréquence de l’onde est égale à celle du vibreur.

Comparaison de l’état vibratoire de deux points

Soient deux points $M$ et $N$ du milieu, séparés d’une distance $M N$ :

Si $M N = k λ avec k \in Z,$ alors les points $M$ et $N$ vibrent en phase.
Si $M N = (k + \frac{1}{2}) λ avec k \in Z,$ alors les points $M$ et $N$ vibrent en opposition de phase.

Vitesse d’une onde sonore

Pour mesurer la vitesse d’une onde sonore, on utilise deux microphones et un oscilloscope. En déplaçant le microphone $R_{2}$ d’une distance $d$ jusqu’à ce que les signaux soient à nouveau en phase pour la $n$ -ième fois ( $n \in N^{*}$ ), on obtient :

λ = \frac{d}{n}

Le décalage temporel $Δ t$ entre deux signaux successifs en phase permet de déterminer la période :

T = n Δ t

On en déduit la vitesse de propagation par :

V = \frac{λ}{T}

Phénomène de diffraction

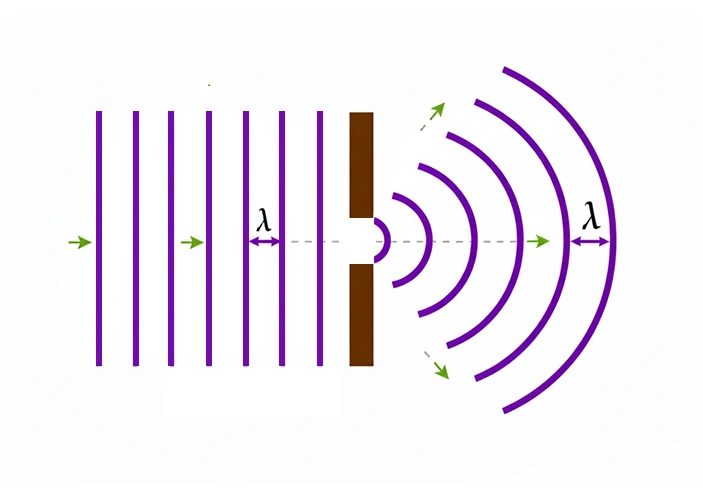
Lorsqu’une onde progressive sinusoïdale rencontre une ouverture (ou un obstacle) de largeur $a$ , sa direction de propagation peut être modifiée : c’est le phénomène de diffraction.

Ce phénomène est nettement observable lorsque :

a \leq λ

Après diffraction, l’onde conserve :

la même fréquence,
la même longueur d’onde,
la même vitesse, à condition que le milieu de propagation reste identique.

Milieu dispersif

Un milieu est dit dispersif lorsque la vitesse de propagation de l’onde dépend de sa fréquence.

Exemple de milieu dispersif : la surface de l’eau (les ondes de grande longueur d’onde se propagent plus vite).
Exemple de milieu non dispersif : l’air pour les ondes sonores (toutes les fréquences se propagent à la même vitesse, $\approx 340 {m·s}^{- 1}$ à 20 °C).