Les Ondes mécaniques progressives

Définition d'une onde mécanique progressive

• Onde mécanique : Il s'agit d'un phénomène par lequel une perturbation se propage dans un milieu matériel élastique sans transport de matière, mais avec transport d'énergie.

• Onde mécanique progressive : C'est une succession continue de signaux mécaniques, résultant d'une perturbation entretenue et continue de la source d'onde.

  
  

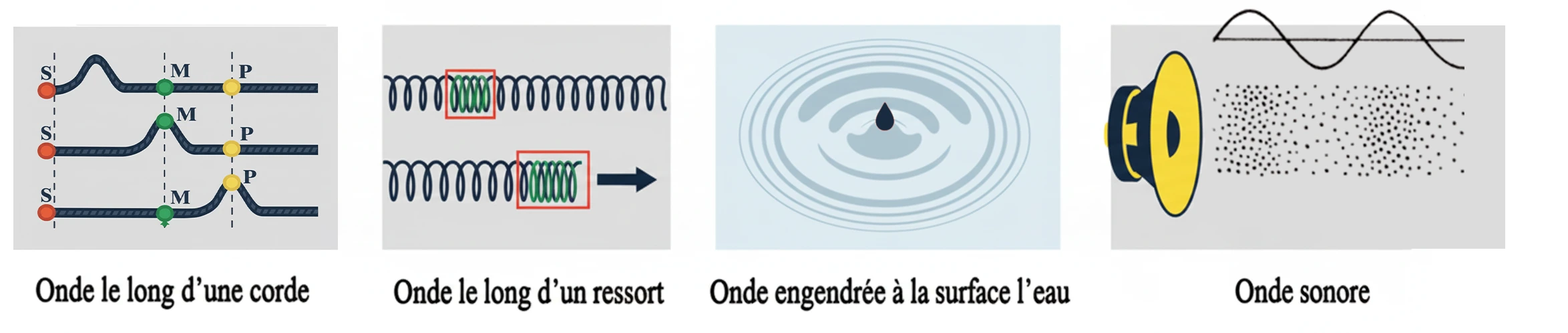
  Types d'ondes mécaniques progressives

  
  

• Onde transversale : La direction de la perturbation du milieu est perpendiculaire à la direction de propagation.
  → Exemples : onde le long d'une corde, onde à la surface de l'eau.

• Onde longitudinale : La direction de la perturbation du milieu est alignée avec la direction de propagation.
  → Exemples : onde le long d'un ressort, onde sonore.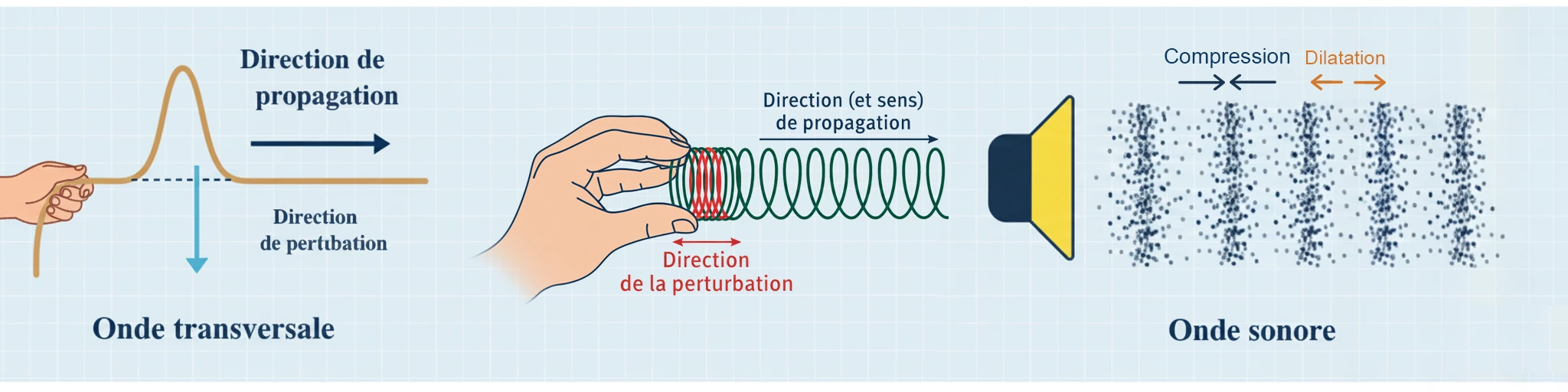

  
  

Propriétés générales d'une onde mécanique progressive

• Direction de propagation : Une onde se propage, à partir de sa source, dans toutes les directions qui lui sont offertes.

• Onde à une dimension : La propagation a lieu dans une seule direction (ex. : corde, ressort).

• Onde à deux dimensions : La propagation a lieu dans un plan (ex. : vague à la surface de l'eau après un jet de pierre).

• Onde à trois dimensions : La propagation a lieu dans l'espace à trois dimensions (ex. : onde sonore).

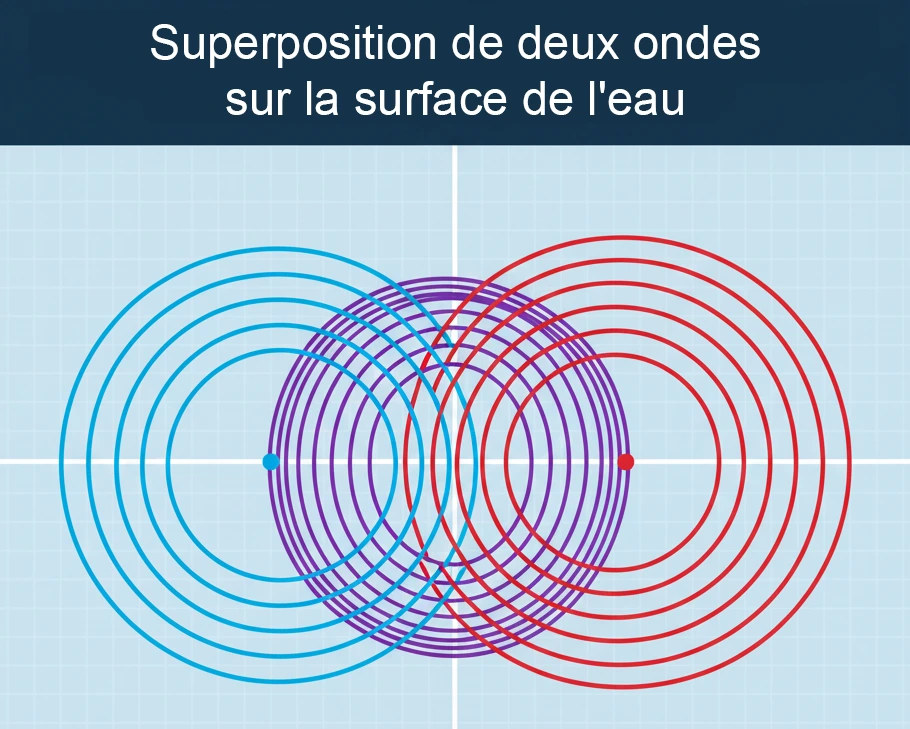
• Superposition de deux ondes : Lorsque deux ondes mécaniques de faible amplitude se croisent, elles se superposent temporairement puis continuent à se propager sans se perturber.

  
  

Vitesse de propagation d'une onde

La vitesse de propagation $v$ d'une onde mécanique progressive est définie par la relation :
$$v = \frac{d}{\Delta t}$$
où $d$ est la distance parcourue et $\Delta t$ la durée de propagation.

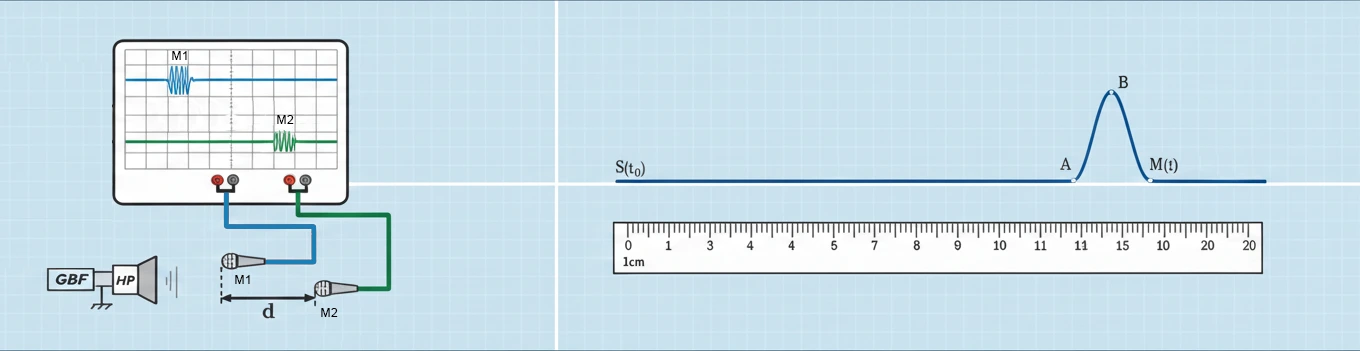
Retard temporel

Lors de la propagation d'une onde mécanique non amortie, chaque point du milieu reproduit le mouvement de la source avec un retard $\tau$.

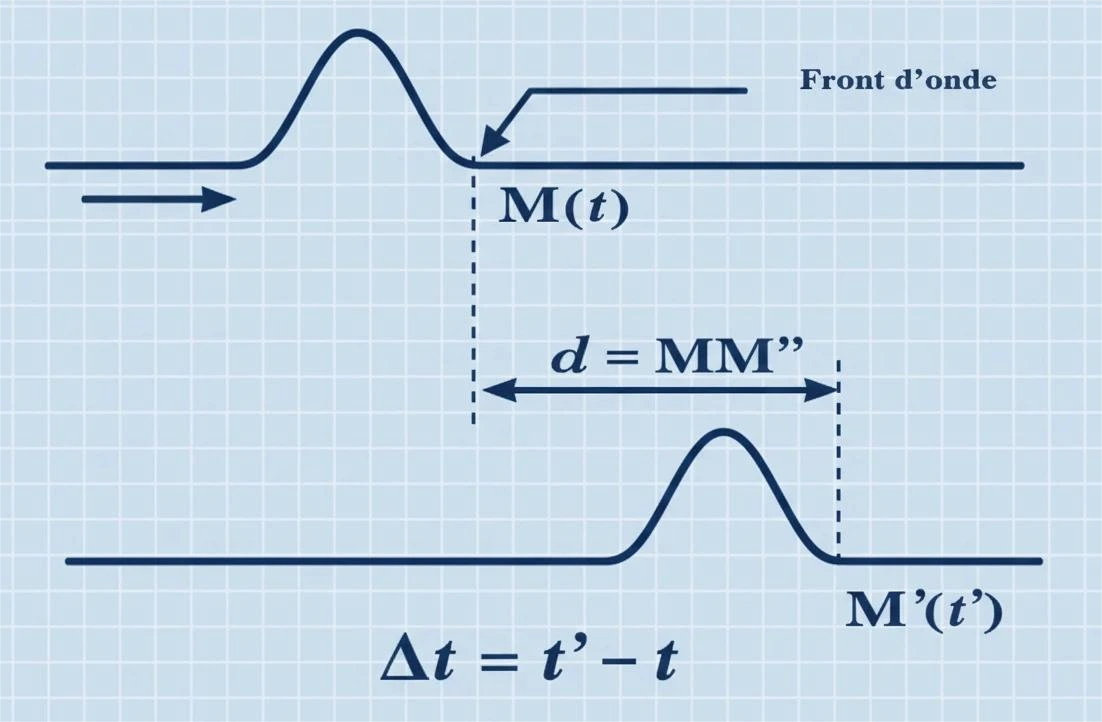
Le retard du point $M$ par rapport à la source $S$ est :
$$\tau = \frac{SM}{v}$$
Plus généralement, le retard du point $M'$ par rapport à un point $M$ est :
$$\tau = \frac{MM'}{v}$$

Élongation d'un point du milieu

L'élongation $y_M(t)$ d'un point $M$ à l'instant $t$ est égale à l'élongation de la source à un instant antérieur :
$$y_M(t) = y_S(t - \tau)$$